supported by the National Science Foundation (DMS-0353880)

|
supported by the National Science Foundation (DMS-0353880) |
 |
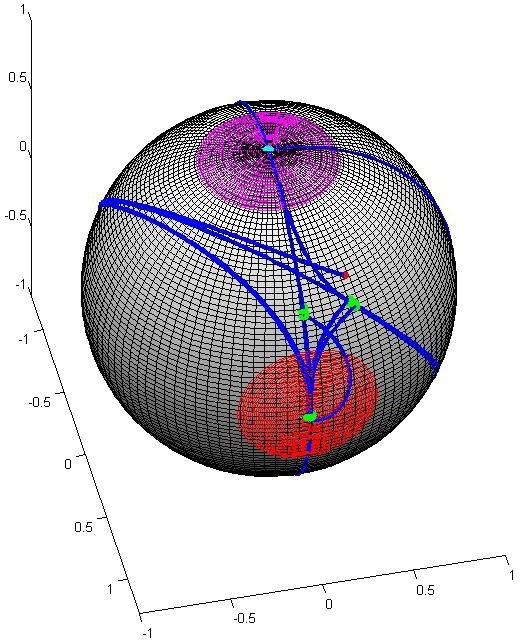
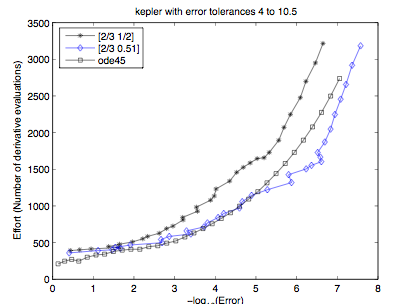
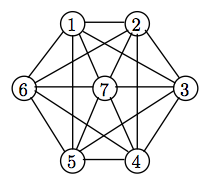
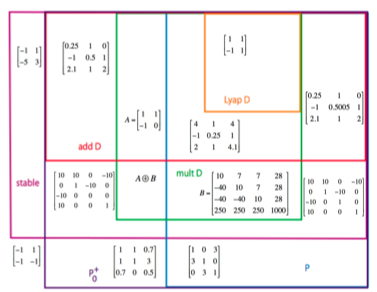
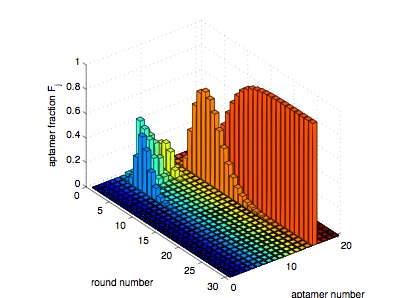
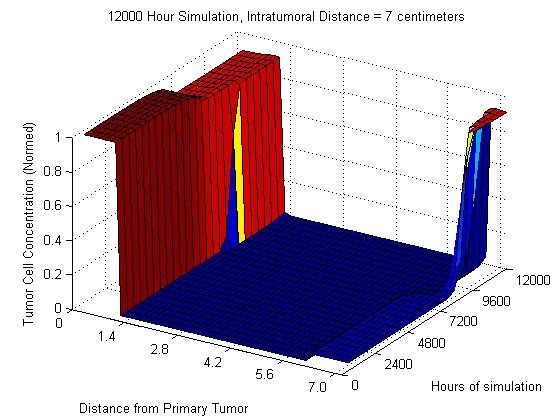
Young
Mathematicians Conference at Ohio State
Undergraduate
Conferences at U Nebraska
Rose-Hulman
Undergraduate Math Journal
Caltech Undergrad
Research Journal
Journal of Young Investigators
Mathematics
Department
Homepage
Web page maintained by Leslie
Hogben
Last Update: 4-May-07