Tumor Angiogenesis
Laura Lutz is a student at the University of Chicago
Erica Naves is a student at Florida A& M University, 
Professor Howard Levine is a Distinguished Professor and is a potential mentor for 2004.
The students began by learning some cell biology and organic chemistry.  They modeled the onset of tumor angiogenesis with a system of partial differential equations. The model focuses on the breakdown of fibronectin and movement of endothelial cells along the capillary wall as critical steps in the formation of new capillaries.  It uses the principles of chemical kinetics and random walks to describe those processes.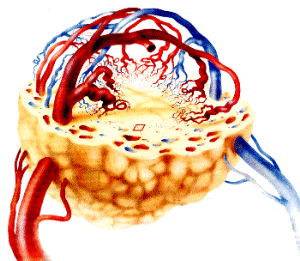 

A highly vascularized tumor (taken from http://www.maths.dundee.ac.uk/~sanderso/tumour.htm)
The model appears to be more accurate than other models in certain respects.  Laura and Erica's paper was entitled A Rigorous Mathematical Model for Tumor Angiogenesis and the Inhibition of Angiogenesis and is being revised for submission.  There are many aspects of this problem for future REU students to study.
 

Evolutionary Robotics

Elizabeth Blankenship is a student at Iowa State University
Jonathan Gandrud is a student at Iowa State University
Professor Dan Ashlock  is a member of the Bioinformatics program at ISU and is a potential mentor for 2004.
This project involved computer simulation of evolution.  Evolutionary algorithms are computer-based problem solving systems that emulate features of biological evolution to produce a sort of software evolution.  The students worked with virtual robots that build and paint (see sample), and cannibal robots.  The latter dealt with a population of 200 virtual autonomous agents (kanibots) that live on a simple grid; they evolved to perform the task of eating each other.  The experiments are related to the well-known prisoner's dilemma, which has also been studied by computer simulation.  Their study serves as additional evidence for a form of general adaptation in evolutionary computation systems using an agent-vs-agent competitive fitness function.  The students wrote individual final REU papers (Elizabeth's was Experimentation with Evolutionary Robots and Building Structures and Jonathan's was  A Note on General Adaptation in Populations of Cannibal Robots).  They also collaborated with Prof. Ashlock to produce a paper A Note on General Adaptation in Populations of Painting Robots, which has been accepted for presentation at the 2003 Congress on Evolutionary Computation to be held in Australia and will appear in the proceedings of the conference.

Nonnegative P-Matrix Completion Problem
Job Evers is a student at Massachusetts Institute of Technology
Steve Shaner is now (fall 2004) a graduate student at Iowa State University
Professor Leslie Hogben is the leader of the ISU Combinatorial Matrix Theory Research Group, co-director of the summer 2004 REUand is a potential mentor for 2005.
A partial matrix is a matrix in which some entries are specified and others are not.  A completion of a partial matrix is a matrix obtained by choosing values for the unspecified entries.  This project examined the completion problem for the class of nonnegative P-matrices.  A matrix is a P-matrix if the determinant of every principal submatrix is positive, and a matrix is nonnegative if all entries are nonnegative.  Together with Prof. Hogben they have submitted a paper entitled The Positive and Nonnegative P-matrix Completion Problems. These results were also presented at the 11th annual meeting of the International Society, Coimbra, Portugal, July 2004. 
Modular Pascal Triangle
Doug Doan is a student at Iowa State University
Tiya Sykes is a student at  Florida A& M University

Professor Jonathan Smith is the Director of Graduate Studies for the Department of Mathematics and is a potential mentor for 2004

Pascal's Triangle read to a prime modulus leads to some standard fractal objects such as the Sierpinski gasket.  Doug and Tiya produced the following picture of the Pascal triangle mod 2 using Matlab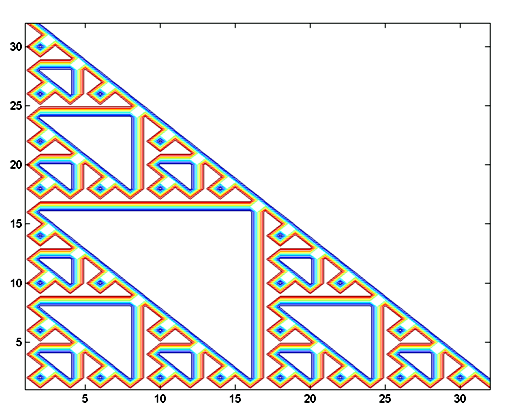

for their paper entitled The Modular Pascal's Triangle. In addition to exploring ideas in the literature, they investigated Pascal's Triangle modulo a composite number, investigating the appropriate tile size to reproduce patterns. There are many questions coming out of this project, which would be fertile ground for projects in future years.
 

Operator Theory

Eric Blabac is a 2003 graduate of ISU and is currently a graduate student in mathematics at ISU.

Lonnie Colbert is a student at Jackson State University

Professor Justin Peters is the chair of the Department of Mathematics and is a potential mentor for 2004.

This project was entitled Iterating Analytic Self-Maps of Discs and Applications to Dynamical Systems.  It was based on a paper by Robert Burkel in the Monthly. The main idea behind the paper was to use the notion of conjugacy of dynamical systems to convert the not so transparent situation with Mobius maps  on the unit disc to a very simple system in the upper half plane. The Mobius maps are classified as elliptic, parabolic, or hyperbolic, and the results in each case are different.  The students also wrote a program in Matlab to model the results, and see if they agreed with the theory.  There are several aspects of the project that were
not investigated, such as sensitivity near the fixed points, that would be viable projects for summer 2004.